研究紹介のページに戻る

汎用シーイングモニター装置の開発とシーイング測定

１．研究の目的と意義

　近年の技術の進歩は、アダプティブオプティクスをして、地上観測における大気揺らぎによる影響をかなり良く改善できるまでになった。しかし、そのような技術でも、完全な画像情報の回復を望むことは不可能である。そのエラーは一般に大気揺らぎの影響が大きい時には大きく、揺らぎが小さい時には小さくなるはずである。ここで重要なことは、観測データを取得した時間における大気揺らぎの程度を如何にして把握し、データ解析や得られた観測結果に対する評価に結び付けるかである。
　大気による光波面揺らぎの性質を明らかにし、観測サイトにおける運用データや観測データの信頼性を評価する知見を得るためには、波面揺らぎの位相構造関数とコヒーレンス時間とをモニターできる測定光学系と観測装置の開発が必要である。しかし、これまでの研究では、既存サイトにある望遠鏡にアダプティブオプティクスの波面センサーを流用した一過性の測定や、口径数十cmの小型望遠鏡の開口面に２つのサブ開口を持ったマスクを取り付けたような簡易的な測定（これではパラメータが一つだけの極めて単純な位相構造関数モデルしか適用できない）に限られてきた。
　観測サイトのシーイング環境を把握し、望遠鏡の運用に活かすためには、より現実的な位相構造関数モデルを適用した大気揺らぎパラメータの測定と同時に、できるだけ日常的なシーイング測定とデータの蓄積が望ましい。従って小型〜中型口径望遠鏡に対して通用するようなスケーラビリティのあるシーイング測定の方法を提案し、それに準拠した測定装置の規格を提案することは、大変意義深いことと考えられる。

２．研究計画

・本装置の性格
・開発体制
・西はりま天文台におけるシーイング測定
・装置の概略
・測定原理

−本装置の性格−（戻る）

　後述する新しい測定光学系（４つのサブ開口を持つ）を用いたシーイング測定装置を開発する。この測定装置により、位相構造関数の power index と outer scale，structure constant（fried parameter），シーイングサイズといった複数の大気揺らぎパラメータを測定する。
　この装置はF比10程度の望遠鏡なら取り付け可能な汎用のものとして設計する。これを既存サイトの望遠鏡に取り付ければ、そのサイトにおけるシーイングコンディションを把握するための初歩的な調査に用いることができる。様々な条件のサイトに持ち込むことにより、観測データの信頼性を評価する上で有用な観測環境パラメータを見つけだすことができるであろう。
　一方で、口径30cmクラスの望遠鏡（F比10程度）にも取り付け可能にして、ポータブルシーイングモニター装置を構成できるようにする。これによって、サイトサーベイ用途や、既存サイトでの初歩的・継続的なモニタリングに活用できる。

−開発体制−（戻る）

　西はりま天文台には、光学実験設備がない。そのため製作は、光学機器の専門業者に発注して行いたい。共同研究者それぞれの役割は以下のように考えている。
光学系概念設計 ：圓谷（西はりま天文台），高見（国立天文台）
装置詳細設計 ：坂元（みさと天文台，元西村製作所），選定業者（未定）
製作・改良 ：業者，坂元，時政（西はりま天文台），圓谷
データ取得システム：圓谷，近田（国立天文台）
データ処理 ：圓谷

−西はりま天文台におけるシーイング測定−（戻る）

　国立天文台の高見英樹氏や高遠徳尚氏らのグループと協力して、汎用性のあるシーイングモニターとして本装置を開発し、それぞれのプロジェクトで活用して行きたい。兵庫県立西はりま天文台公園では、施設拡充の一貫として、西はりま天文台に２m望遠鏡を建設すべく準備を進めてきている。新設天文台の基礎調査、完成後の観測をサポートする装置として、本装置のようなシーイング測定装置を開発する必要に迫られている。
　具体的には、西はりま天文台60cm望遠鏡に、開発したシーイング測定装置を取り付けてシーイングの測定を行い、所定の大気揺らぎによるパラメータ（位相構造関数の power index と outer scale，structure constant（fried parameter），シーイングサイズ）を導けることを確認する。続いて、シーイング測定のモニタリングを開始する。
　本装置によるシーイング測定の利便性が確認できた後に、国立天文台の他プロジェクトや各公開天文台など、より多くの要求に応じて本装置もしくは改良・発展版を提供し、活用してもらうための次段階について検討したい。

−装置の概略−（戻る）

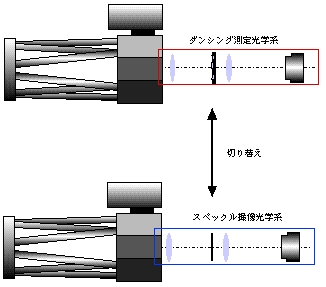
・測定光学系（図１）
　望遠鏡焦点近くで光束をコリメートした後、ダンシング測定モードでは、平行光を光学ウエッジ付きの４開口アパーチャーマスクに通し、各サブアパーチャー毎に独立した星像を結像させて、ビデオカメラで星像のダンシングを記録する。スペックル撮像モードではnarrow-band フィルタをはさんだ拡大光学系で星像を結像して、同じカメラで speckle像を記録する。

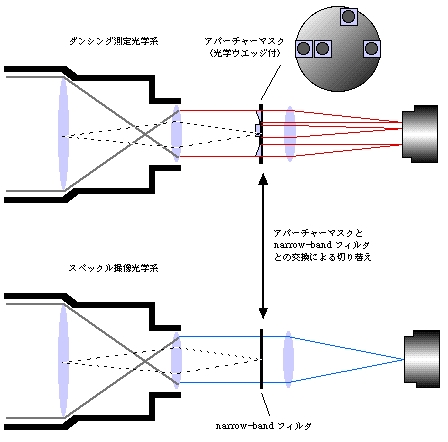
　この時、望遠鏡のF比が同じであれば平行光束の直径は同じであるため、アパーチャーマスクやnarrow-band フィルタは同じサイズのものが使用できる。また、これらのマスクを挿入する位置は、コリメータレンズからの距離 s が

　f_c：コリメータレンズの焦点距離，f_t：望遠鏡の焦点距離

であることからわかるように、大きく変わらないため調整可能である。

・光学系の概略（戻る）
１）像面スケール

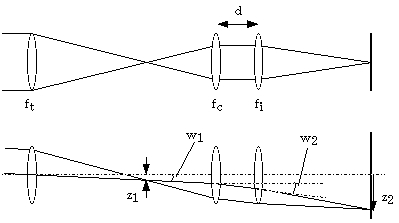
像面スケール s は、

　　[arcsec/mm]

と表される。ここで d は、この間にアパーチャマスクや干渉フィルターを挿入することを考えると、

でなければならない。

２）西はりま天文台60cm望遠鏡の場合のパラメータ

60cm望遠鏡の焦点距離　f_t=7200mm
平行光束のサイズを20mm程度にするため、
コリメータレンズの焦点距離　f_c=150mm
画像をピクセルサイズ12μmのディテクタでサンプリングすると、サンプリングサイズ I_pix は、 　　[arcsec/pix]

となる。これより結像レンズ

f_i=300mm とする時、I_pix=0.174[arcsec/pix]

　

３）30cm（F10）望遠鏡の場合

f_i=600mm とする時、I_pix=0.208[arcsec/pix]

−測定原理−（戻る）

１）光波面の揺らぎと位相構造関数
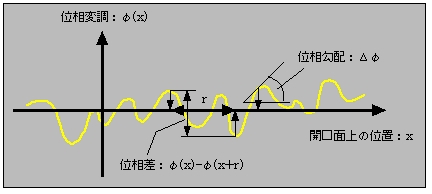
　地球大気層の屈折率の揺らぎは、望遠鏡開口に届く光の光路長を光路毎に変調し、光波面をランダムに凹凸させてしまう。この光波面の凸凹の構造を定量的に表現する物理量として、位相構造関数が以下のように定義されている。

φ(x)：ｘでの位相の変調量

２）difference構造関数の測定１（戻る）
　開口面上で距離ｒ離れた２点における位相勾配の差の二乗平均をdifference構造関数：DΔφ(r)という（Dayton, 1992¹ ）。

Δφ(x)：ｘでの位相勾配

　この物理量はＡＯのシャックハルトマンセンサーに利用されているマイクロレンズアレイ光学系を使って測定することができる（図３）。位相勾配は、焦点面上に結ばれた各マイクロレンズの星像のダンシング（光軸からのずれ）として検出される。

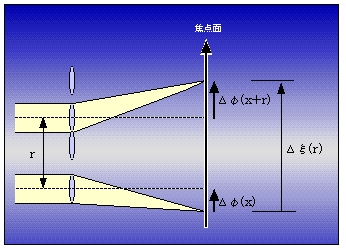
ところで位相勾配を測定するとき、レンズアレイ像のスナップショット毎、暗い星像（スポット）の中心位置をいちいち測定するのは、煩雑であり精度を出すのも大変である。ここで目的であるdifference構造関数の定義をよくよく見ると、DΔφ(r) は２つのスポットの相対位置Δξ(r)の分散であることがわかる。一般に位置の分散は、長時間露光像の星像の広がりとして現れるはずのものである。

３）difference構造関数の測定２（戻る）
　以上の事から、difference構造関数は speckle干渉法で用いられる Shift and Add法を応用することで、画像処理的に測定することができる。図４は独立した２つの開口のつくる星像を、一方のスポットを refernce として Shift and Add した画像の一次元輝度分布の模式図である。

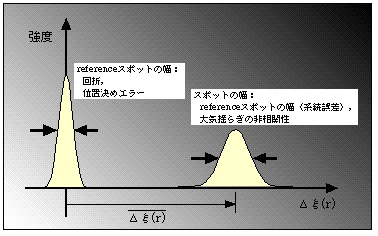
図のように、referenceスポットの幅は、開口で決まる回折とShift and Add するためのスポット中心の決定精度によって生じる。これを系統誤差として、もう一方のスポット像は、大気揺らぎの非相関性のため、 referenceスポットに対するダンシングによっても拡がる。したがって両方のスポットの拡がりを比較することによって difference構造関数の測定値から系統誤差を取り除くことができる。このように Shift and Add法を応用することで、大気揺らぎ測定のための情報処理を、単純かつ精度良く行うことができるだろう。

４）位相構造関数の決定（戻る）
　difference構造関数は、位相構造関数

φ(x)：ｘでの位相の変調量

とのあいだに

という関係を持つ。これより、位相構造関数のモデルに従って
・Dφ(r) ∝ r^p （Kolmogorov近似的）のとき

あるいは、
・Dφ(r) ∝ 1-exp(-r²/L0²)　（Mckechnie近似的：L0≡揺らぎの outer scale）のとき

をフィッティングすることにより、位相構造関数の power index もしくは outer scale を求めることができる。別に星像のシーイングサイズを測定して、位相揺らぎの相関が２πを超えるスケールサイズ（structure constant/Fried parameter：r0）を見積もれば、位相構造関数を観測的に決めることができる。

　さらに、４つのサブアパーチャーを持つ装置の意義として、Kolmogorov近似（Power-low による漸増モデル）とMckechnie近似（漸近的に収束するスケールを持つモデル）の両方の性格を持たせたモデル例えば

のようなより現実的なモデルを適用して、複数のパラメータを決められる事を強調しておきたい。

¹ D. Dayton et al. Opt. Lett. Vol.17 No.24, 1737 (1992)